백준 주유소[13305번]
문제
어떤 나라에 N개의 도시가 있다. 이 도시들은 일직선 도로 위에 있다.
편의상 일직선을 수평 방향으로 두자. 제일 왼쪽의 도시에서 제일 오른쪽의 도시로 자동차를 이용하여 이동하려고 한다.
인접한 두 도시 사이의 도로들은 서로 길이가 다를 수 있다. 도로 길이의 단위는 km를 사용한다.
처음 출발할 때 자동차에는 기름이 없어서 주유소에서 기름을 넣고 출발하여야 한다.
기름통의 크기는 무제한이어서 얼마든지 많은 기름을 넣을 수 있다. 도로를 이용하여 이동할 때 1km마다 1리터의 기름을 사용한다.
각 도시에는 단 하나의 주유소가 있으며, 도시 마다 주유소의 리터당 가격은 다를 수 있다. 가격의 단위는 원을 사용한다.
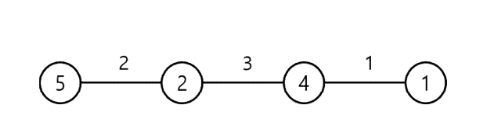
예를 들어, 이 나라에 다음 그림처럼 4개의 도시가 있다고 하자. 원 안에 있는 숫자는 그 도시에 있는 주유소의 리터당 가격이다.
도로 위에 있는 숫자는 도로의 길이를 표시한 것이다.
제일 왼쪽 도시에서 6리터의 기름을 넣고, 더 이상의 주유 없이 제일 오른쪽 도시까지 이동하면 총 비용은 30원이다.
만약 제일 왼쪽 도시에서 2리터의 기름을 넣고(2×5 = 10원) 다음 번 도시까지 이동한 후 3리터의 기름을 넣고(3×2 = 6원) 다음 도시에서 1리터의 기름을 넣어(1×4 = 4원) 제일 오른쪽 도시로 이동하면, 총 비용은 20원이다.
또 다른 방법으로 제일 왼쪽 도시에서 2리터의 기름을 넣고(2×5 = 10원) 다음 번 도시까지 이동한 후 4리터의 기름을 넣고(4×2 = 8원) 제일 오른쪽 도시까지 이동하면, 총 비용은 18원이다.
각 도시에 있는 주유소의 기름 가격과, 각 도시를 연결하는 도로의 길이를 입력으로 받아 제일 왼쪽 도시에서 제일 오른쪽 도시로 이동하는 최소의 비용을 계산하는 프로그램을 작성하시오.
입력
표준 입력으로 다음 정보가 주어진다. 첫 번째 줄에는 도시의 개수를 나타내는 정수 N(2 ≤ N ≤ 100,000)이 주어진다.
다음 줄에는 인접한 두 도시를 연결하는 도로의 길이가 제일 왼쪽 도로부터 N-1개의 자연수로 주어진다.
다음 줄에는 주유소의 리터당 가격이 제일 왼쪽 도시부터 순서대로 N개의 자연수로 주어진다.
제일 왼쪽 도시부터 제일 오른쪽 도시까지의 거리는 1이상 1,000,000,000 이하의 자연수이다.
리터당 가격은 1 이상 1,000,000,000 이하의 자연수이다.
출력
표준 출력으로 제일 왼쪽 도시에서 제일 오른쪽 도시로 가는 최소 비용을 출력한다.
서브태스크
| 번호 | 배점 | 제한 |
|---|---|---|
| 1 | 17 | 모든 주유소의 리터당 가격은 1원이다. |
| 2 | 41 | 2 ≤ N ≤ 1,000, 제일 왼쪽 도시부터 제일 오른쪽 도시까지의 거리는 최대 10,000, 리터당 가격은 최대 10,000이다. |
| 3 | 42 | 원래의 제약조건 이외에 아무 제약조건이 없다. |
예제 입출력
입력 1
1
2
3
4
2 3 1
5 2 4 1
출력 1
1
18
입력 2
1
2
3
4
3 3 4
1 1 1 1
출력 2
1
10
풀이
1
2
3
4
5
6
7
8
9
10
11
12
13
14
import sys
city_num=int(sys.stdin.readline().rstrip())
bridge=list(map(int,sys.stdin.readline().rstrip().split(" ")))
city=list(map(int,sys.stdin.readline().rstrip().split(" ")))
minPrice=city[0]
total=0
for i in range(city_num-1):
if minPrice>city[i]:
minPrice=city[i]
total+=(minPrice*bridge[i])
print(total)
설명
처음에는 전체 도시중에 가장 기름값이 싼 도시를 찾고, 그 도시 뒤에 있는 모든 도로들을 해당 도시의 기름값으로 사면서
도로를 뒤에서 앞으로 없애는 방식을 사용하였다.
하지만 처음의 방식은 이중 반복문을 사용해서, 최악의 경우 O(N^2)의 시간복잡도를 가진다.
그래서 처음에는 시간초과가 났었다.
하지만 단일 반복문, 즉 O(N)으로도 충분히 해결이 가능한 문제였고, 심지어 어렵게 생각할 필요도 없었다.
그저 처음 도시에서부터 끝에 도시까지 순차적으로 가야하므로, 순차적으로 가면서 매 순간 제일 기름값을 선택하면서 도시를 방문하면 된다.
즉 그리디 알고리즘 중 가장 간단한 구조라고 볼 수 있다.